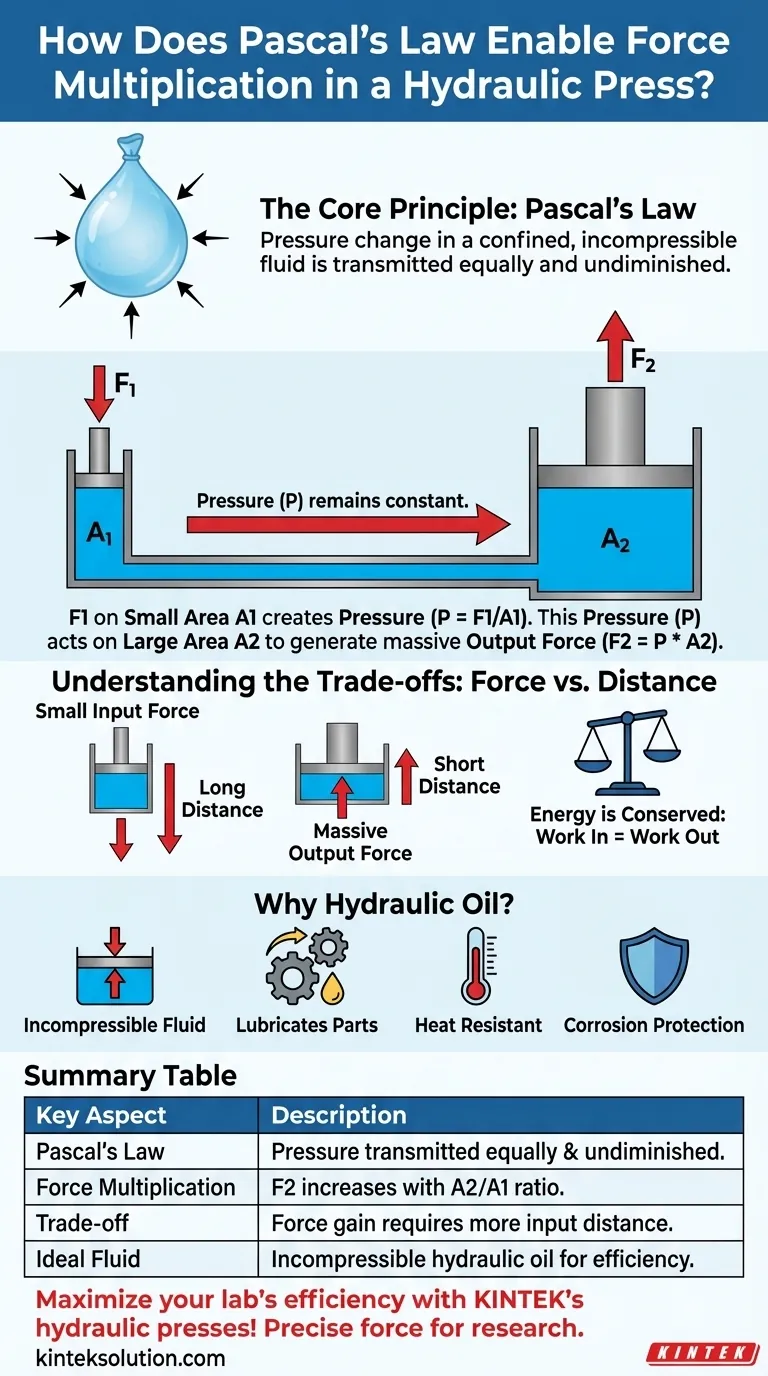
在液压机中,力是通过利用密闭的、不可压缩的流体将压力从一个小面积传递到一个大面积来实现倍增的。当一个小输入力施加到一个小活塞上时,它会在流体中产生压力。相同的压力随后作用于一个大得多的活塞上,从而产生一个明显更大的输出力。
液压系统不会创造能量;它用距离来换取力。通过在一个输入活塞上施加一个作用于长距离的小力,您会产生一个巨大的力,使输出活塞移动很短的距离,所有这些都受制于密闭流体中压力保持恒定的原理。
核心原理:帕斯卡定律解释
什么是帕斯卡定律?
帕斯卡定律是液压学的基本原理。它指出,在密闭的、不可压缩的流体中任何一点的压力变化都会等量且不减弱地传递到流体的每一部分及其容器壁。
压力传输的可视化
想象一下挤压一个密封的水球。您用手指施加的压力会被整个气球表面均匀地感受到,而不仅仅是您挤压的那个点。液压系统遵循相同的原理,但在一个更受控的环境中运行。
不可压缩流体的作用
为了使该定律有效,流体(通常是特种油)必须是不可压缩的。这意味着其体积在压力下不会明显减小。这确保了施加的力被用来移动活塞,而不是压缩流体本身。

液压机如何实现力倍增
双活塞系统
液压机由两个连接的气缸组成,每个气缸都有一个不同尺寸的活塞。较小的活塞是输入活塞(或柱塞),初始力施加于此。较大的活塞是输出活塞(或柱塞杆),它执行工作。
步骤 1:产生压力
压力 (P) 定义为施加在面积 (A) 上的力 (F),即 P = F/A。当一个小力 (F1) 施加到具有面积 A1 的小输入活塞上时,它会在流体中产生压力。
步骤 2:传输压力
根据帕斯卡定律,此压力 (P) 会等量地传输到整个液压流体中。存在于小活塞下方的压力现在存在于大输出活塞下方。
步骤 3:产生输出力
这个恒定压力 (P) 现在作用在输出活塞的较大面积 (A2) 上。所得的输出力 (F2) 可以计算为 F2 = P * A2。因为 A2 远大于 A1,所以 F2 相对于初始输入力 F1 成比例地变得大得多。
例如,如果输出活塞的表面积是输入活塞的 20 倍,则输出力将是输入力的 20 倍。
理解权衡:没有“免费午餐”
能量守恒
液压倍增似乎是无中生有,但它完全遵守能量守恒定律。在输入侧所做的功必须等于在输出侧所做的功(忽略摩擦造成的微小损失)。
真正的代价:力与距离的交换
功的计算方式是 功 = 力 x 距离。为了实现巨大的输出力,您必须以距离为代价。
为了实现 20 倍的力倍增,小输入活塞必须移动的距离比大输出活塞移动的距离远 20 倍。您是用一个长的、省力的推力来换取一个短的、强有力的推动。
为什么液压油是理想选择
虽然水在理论上可行,但特种液压油之所以被使用,不仅因为它们不可压缩,还因为它们可以润滑系统的运动部件、防止腐蚀,并具有高沸点以抵抗摩擦和压力产生的热量。
为您的应用做出正确的选择
了解核心原理可以帮助您了解液压系统是如何针对特定任务进行定制的。
- 如果您的主要重点是最大化力: 关键是最大化输出活塞(柱塞杆)与输入活塞(柱塞)之间的面积比。
- 如果您的主要重点是系统设计: 请记住,每增加一倍的力,行程距离就会按比例减小。您必须在动力和所需的运动范围之间取得平衡。
- 如果您的主要重点是排除“海绵状”系统的故障: 最可能的原因是液压管路中夹带了空气。空气是可压缩的,因此施加的力会浪费在挤压气泡上,而不是被有效地传输。
通过掌握压力、面积和距离之间简单而深刻的关系,您可以利用液压系统的巨大动力。
总结表:
| 关键方面 | 描述 |
|---|---|
| 帕斯卡定律 | 密闭流体中的压力变化等量且不减弱地传递。 |
| 力倍增 | 输出力随活塞面积增大而增加,例如,面积比为 20 倍,力增加 20 倍。 |
| 权衡 | 力的增加要求输入活塞移动得更远;能量守恒。 |
| 理想流体 | 不可压缩的液压油确保高效的压力传输和系统保护。 |
使用 KINTEK 的液压机最大限度地提高您实验室的效率! 我们的全自动实验室压机、静水压机和加热实验室压机旨在为您研究和测试需求提供精确的力倍增。体验可靠的性能和定制的解决方案——立即联系我们,讨论我们如何支持您的实验室目标!
图解指南
相关产品
- 全自动实验室液压机 实验室压粒机
- 用于 KBR 傅立叶变换红外光谱仪的 2T 实验室液压压粒机
- 实验室液压压力机 实验室颗粒压力机 纽扣电池压力机
- 手动实验室液压机 实验室颗粒压制机
- 用于 XRF 和 KBR 颗粒压制的自动实验室液压机



















